| ブレーキの勘違い | |||||||||||
|
友人のブレーキが「カチカチ」だった。 なぜかを考えて、マスターとキャリパーのサイズが合っていないという推論に至った。 で、質問したら、その通り。 なのだが、なぜそれじゃダメなのかが説明しにくい。 いろいろ考えていると、感覚的に変な気がする。 しかし、変に感じるのはブレーキに関する要素がいっぱいありすぎて混同するからなのだ。 1個1個別にして考えると、あたりまえの説明ができる。 ただし、ブレーキって確か整備士資格ないと触っちゃいけないものだから、触らないでね。単なる知識としてどうぞ。 |
|||||||||||
|
後から気がついた。 デカい方がいいと思うなら、キャリパーのピストンと同じ口径のマスター使ったら、なにが起こるか考えてみればいいんじゃない? |
|||||||||||
| マスター径の差 | |||||||||||
|
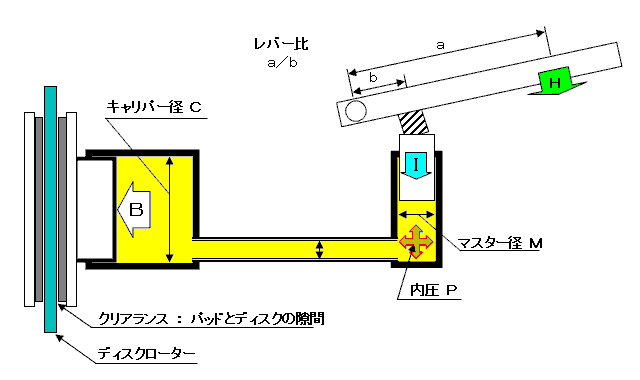
レバーを握る力をHとする。 レバー比がa:b=8:1とすると、マスターのピストンに加わる力は8Hとなる。 Hを、30kgと仮定すると、240kgの力がIとして入力される。 この240kgはマスター径が11mmのときなら、面積は(11/2)^2π=30.25π平方ミリだから、240kg/30.25π平方ミリ=7.93/π kg/平方ミリの圧力を生じる。 キャリパー径が30mmとすると、面積は(30/2)^2πだから、225π平方ミリ。 225π平方ミリ×7.93/πkg/平方ミリとなりパッドには1,784.25kgの力がかかる。 ここで同じようにマスター径を14mmで計算すると、 キャリパー径(30/2)^2π/マスター径(14/2)^2π×入力240kg=1,102.0kg の力がかかる。 この力の差は、テコの原理で発生するから、キャリパー径/マスター径で決まって、マスター径が大きいほど力は弱くなる。 しかも、おそらく、マスター径が大きいとこれ以上に力は弱くなる。 なぜなら、内部の圧力が同じ 7.93/π kg/平方ミリだったとする。 これを、マスター側を押し戻そうとする反力とみると、 14mm径のとき、 (14/2)^2π×7.93/π kg/平方ミリ=388.57kg 11mm径のとき、 (11/2)^2π×7.93/π kg/平方ミリ=239.88kg となって、14mm径のときには、入力の240kgを越えてしまう。 入力が240kgで14mm径を再計算すると、 240kg/(14/2)^2π平方ミリ=4.90/π kg/平方ミリ となって、4.90/7.93=0.62 となって、11mm径のときの6割の力しかかけられなくなる。 この両方の結果から、11mm径ではパッドに1,784.25kgかかっていたのが、実は、 225π平方ミリ×4.90/πkg/平方ミリ=1,102.5kg。 1,102.5:1,784.25=6:10 で、14mm径は11mm径の6割の圧力しかパッドに伝えないのだ。 |
|||||||||||
 |
|||||||||||
| なにか変? | |||||||||||
|
「マスター径が大きいほど弱くなる」ってなにか変? 大きい径のマスターの利用価値は何か? 変ではないのだ。マスターサイズを変えて計算したけど、キャリパーサイズを固定している。 30mm径のシングルポッド(ピストン)キャリパーっていうのはかなり小さい。 スクーター用である。 「マスター径が小さいほど強く締め付けられる」というのは事実だが、「マスター径が小さければ送り出すフルードの量が少なくなる」というのがテコの原理。 レバー比とストロークが同じなら、マスター径が14mmのときは11mmのときの1.6倍のフルードを送り出せる。 送り出す先が30mm径2ポッドなら、さきほどの計算で キャリパー径(30/2)^2π/マスター径(14/2)^2π×入力240kg=1,102.0kg だったものが2ポッドで使うと キャリパー径(30/2)^2π×2/マスター径(14/2)^2π×入力240kg=2,204.1kg になる。 |
|||||||||||
| キャリパーがデカければいいのか? | |||||||||||
|
では、「キャリパー径とマスター径の比が大きいほどよく効く」? それは、力だけならその通り。 だから、間違える。 30mm径2ポッドと11mm径マスターの面積比は マスター径(11/2)^2π:キャリパー径(30/2)^2π×2=1:14.88 だから、マスターを15mm縮めて、キャリパーは約1mm出る。 さらに、対向型4ポッドキャリパなら1/2mmしかピストン=パッドが動かない。 実際には1mmも動けば十分なのだが、レバー比を1:8とすると、マスターを15mm押し込むときには、レバーを120mmも握らなければならない。実際の有効ストロークは50mmもないくらいだろう。 50mm握るとすると、マスターは6mmちょっと沈んで、キャリパーは0.4mm(対向なら0.2mm)動く。 これでは少なすぎるから、14mmマスタを使うと ストローク50mm/レバー比8×マスター径(14/2)^2π/キャリパー径((30/2)^2π×2) =0,68mm 動く。 加わる力は 握力30kg×レバー比8/マスター径(14/2)^2π×キャリパー径((30/2)^2π×2)=2,204.0kg になる。 キャリパーが大きいとテコの比が大きくなって強くなる。 が、テコの比が大きいと動く距離が小さくなるから、マスターも大きくする。だから、 径の大きなマスターは、大型キャリパー用のもの。 |
|||||||||||
| スポンジー | |||||||||||
|
ブレーキにエアを噛んで、最後まで握ってもフワフワしているのを「スポンジー」と言う。 ブレーキフルードは、液体で流動するけれど、圧力によって体積が変わらないような素材でできている。 圧力をかけて体積が小さくなると、マスターが15mm沈んでも、キャリパーが出る量が減ってしまうからだ。 このフルードにエアが混じっていると、フルードの体積は変わらなくても、エアの体積は低い圧力で変わってしまうから、力が有効に伝わらない。最後まで握ってもカッチリしないのは、エアがクッションになっているから。=スポンジー ブレーキのフルードには、上の試算で7.93/π kg/平方ミリ=25kg/平方ミリという相当な圧力が加わる。 この圧力はキャリパーのピストンだけでなくブレーキシステムの部品1つ1つの内側に加わるから、圧力を想定した専用ホースでもほんの少し風船のように膨らむ。 膨らむということは25kg/平方ミリの圧力が逃げることだから、同じ圧力30kgで握ってもブレーキの効きが悪くなる。 この膨らみによるロスを少なくしようとするのがステンメッシュホースである。 |
|||||||||||
| 深みにはまる | |||||||||||
|
さて、ステンメッシュとか言いだすと、問題がわかりにくくなってくる。 今まで、書いてきたことは正しい。その前提に納得してからでないと、この先を読むと、もっとわからなくなる。 今まで、数字を使って説明してきたが、レバー比とか、キャリパーのピストン径とかはそれらしく想像しただけの値である。最終的にパッドにかかる力が、実際にはどのくらいの大きさなのかは、いいかげんである。それでも、仕組みを理解する上では間違っていない。 そこでだ。 まだ先がある。 フルードにかかるのは「圧力」だ。 ブレーキラインが膨らむと圧力が逃げると書いた。 つまり、圧力を決めるのは容積だ! ところが、今までの議論で、容積には触れていない。 それでいいのか? いいのだ。 圧力が問題なら、240kg(これも本当は240kgfなのを無視している)の入力が、25kg/平方ミリという圧力に変わるかどうかは、体積の問題なのだ。 これを、薄々にでも感じている人は、ホースの太さとか長さを気にする。 それは正しい。 11mm径のピストンが50/8=6mmちょっと動くなら、圧力は、 マスター径(11/2)^2π×6mm:全体の容積 で決まるのだから、ブレーキホースも含む全体の容積を知らないと語れない。 が、ブレーキシステムはピストンが動いて、リザーバへの通路が閉じた瞬間で、1気圧の内圧を持っている。この1気圧は、内からも外からも全体にかかっているから、無視する。 リザーバ通路が閉じた瞬間から、ブレーキを握る=ピストンを押し込んでいくと、フルードの内圧が高まるだけ、その力でピストンが押し戻される。ピストンが動いている限り内圧は1気圧!(+ダイアフラムの反力) だから、100kg、200kg、240kgの力がかかったときの内圧は、加えた力から逆算できるのだ。 ブレーキシステム全体のフルードの容量/(ブレーキシステム全体のフルードの容量−ピストンが沈み込んだ体積)=圧力 だが、これは 圧力=レバーに加えた圧力に対向できる力 だから、容積から計算しなくてもいいのだ。逆に言うと、ブレーキシステムの容量がむやみに大きく、マスターのピストンが6mm沈んでもたいした圧力にならなければ、30kgなんて力をかけないうちにレバーはスコッと抵抗なく握れてしまう。握って、どこかで止まるということは、止まったときに握っている力と釣り合う(等しい)圧力があるということ。 だから、スカスカに握れてしまうのでなければ、ブレーキホースの太さや長さは関係ないのだ。(流体を固体でシミュレートしているわけだ) 言い換えれば、今までの計算は、握っていく間の変化を無視して、握りきったときの最大圧力だけを扱っているから変化する容積の複雑な計算を飛ばしているわけだ。 |
|||||||||||
| 太さと長さ | |||||||||||
|
だから、今までの説明で容積をもとに考えてこなくてもいいのだ。 で、太いかな? 長いかな? と心配するべきなのは、スポンジーなとき。 レバーを握りこんで、パッドが接触した瞬間にレバーを止めれば、このときの圧力は1気圧のままだ。レバーが戻ろうとするのはピストンを戻すスプリングやダイアフラムの反力でしかない。 パッドが接触したところから、パッドはそれ以上動かないから、さらに握り込んでいくと、ブレーキシステム内の内圧が上がっていき、パッドをディスクに押し付ける力が強くなっていく。同時に、パッドやキャリパーがほんのわずかだが歪むなどして、力をロスする。 自転車のブレーキみたいなゴムなら抵抗がかかるのも分かるが、ツルツルの金属ディスクと固いパッドが、制動力を生むというのは、それほど高い圧力がかかっているということなのだ。 この、圧力が高まっていく過程がジワリと握りこんでいく「握りしろ」だ。この、圧力の調整で、軽いブレーキや急制動が使い分けられる。 しかし、圧力が異常に高いので、十分に固いと思われるキャリパーやパッドすらしなる。 キャリパーがしなる程度は、キャリパーの筐体の剛性や取り付けの遊びなどとともに計算されていて、制動力に影響は出ないはず。 ここで、ブレーキフルードをさっきから剛体とみなしていていいのは、圧力に対して縮む(圧縮)率が非常に小さい物質を使っているからだが、体積が異常に大きくなれば影響が出てくる。目いっぱい握りこんだときの高圧で0.1%(かどうかしらないが)しか縮まないはずのフルードだとしても、全体の容量が100ccのときには、0.1ccの影響が出る。これが、200ccになると同じ0.1%で0.2ccになる。 どっちにしろ、ほんのわずかな量に思えるが、また、マスタの径を11mmで計算すると、断面積は約0.95平方センチだから、0.1ccの差は約1mmのピストンストロークになる。そして、レバーでは8mmも遊びが増えてしまうわけだ。 30kgの握力を2tの圧力に変換しようとするシステムで、1ccの差は意外とデカい。 これは、フルードがどれだけ縮むかによる影響だが、逆にホースが同じ圧力で0.1%膨らんでも、ピストンの移動量への影響は同じ結果になる。−という風に考えてみても、ブレーキシステム全体の容積に対してホースの影響は何%くらいかとか、フルードの圧縮率よりホースの膨らみ方はどちらが大きいか、などと、考えるべきことがすぐに広範囲に広がって難しくなる− 要するに、必要最低限で固くて短く細いホースがいいのだ。 |
|||||||||||
| だぁ〜からぁ | |||||||||||
|
なにが言いたいかと言えば。 ・ふにゃふにゃ(スポンジー)してれば、ホース、液漏れ、フルードの劣化、エアや水の混入とか ・固いのに効きが悪ければ、パッド、キャリパーの作動不良、マスタがデカ過ぎ、ホースのつまりとか ・カチカチならば、マスタがデカ過ぎるか、なにかとんでもないこと が怪しい。 ブレーキに関しても、マスタとキャリパのタイプやサイズの組み合わせは理由があってメーカーが選んでるんだから変えちゃダメ! 例えば、6ポッド、8ポッドなんてブレーキをつけるにはそれに適したサイズのマスターが必要。 キャリパ側の口径が大きくなれば、マスターをデカくしなくてはならないけど、マスターをデカくするデメリットも減る。今回触れていないことを言えば、キャリパが大きくなれば、パッドの有効面積が大きくなるから、圧力が弱くなってもよく効く可能性もある。ディスクの直径もでかいはずだから、それだけでも制動力は上がる。でも、回転マスは増える。 そんな、いろんなことを考えてマスターのサイズは決まってる。 11mmマスターとそれに合うキャリパーが着いていれば、ディスクの直径もほぼ決まっている。 いたずらに、何かだけ大きくしてもダメ。 何かしたら、何か他の影響が出る。 要するに、パーツを1個だけ変えてもダメ。 |
|||||||||||
|
|
|||||||||||